
Explaining probability using dice
Climate change projections are fundamentally uncertain. However, the UKCP09 report does try to estimate the probabilities behind each change. For example: "...what probability is there that the temperature will change by at least 2ºC by March 2050...?". These probabilistic estimates are not perfect understandings how likely each degree of change is, but they are the best that we have. Baring this in mind, I have decided to use a central, 67% probability band to look at a reasonably likely range of climate change. This is similar to rolling anything between 5 and 9 on two dice. If the projections are accurate, there would be a 1-in-6 chance of that the change is lower / less than the bottom, and a 1-in-6 chance that it is greater / higher than the top of the band.
Rolling two normal dice
The following table shows all of the results that you can get from rolling 2 dice. ![Two 6-sided dice to be precise. Also note that 'die' is the singular of dice. [i]](../images/_info.jpg)
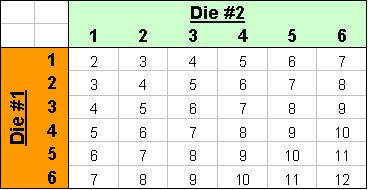
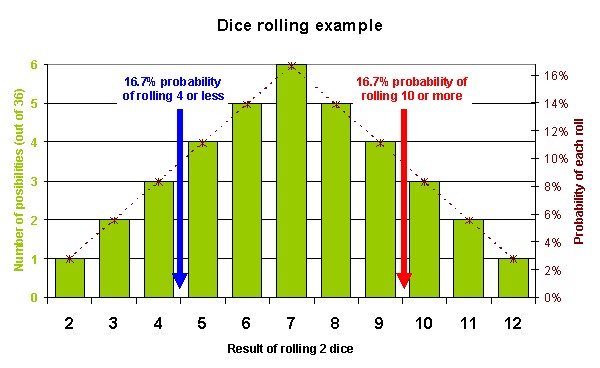
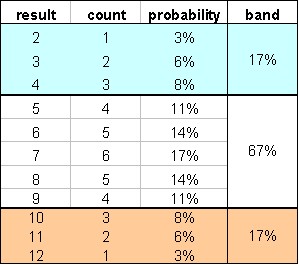
You can take these results and count the number of possible outcomes, for example there are 4 possible combinations of rolling dice that add up to 5 (i.e. 1&4, 2&3, 3&2 and 4&1). The following chart and table show this distribution. A central band of probability is highlighted, based on rolling any result between 5 and 9. There is a 67% chance that this will be the result of my next roll.
What about imperfect dice?
The distribution presented above assumes a perfect world with perfectly random dice (i.e. each die has an equal chance of rolling any number). If my dice are a bit old and knackered, with the corners a bit chipped, they wont be perfect. The real probability distribution will be skewed in some way, as the dice act like they are slightly loaded towards certain results.
To try and understand the probability distribution of these old dice, I would need to analyse the results of lots of rolls and maybe carry out some kind of modelling. This could be a very complex exercise, with a lot of uncertainty in how exactly to draw the probability distribution.
I don't have a model that can tell me how a pair of nearly cube-shaped dice will bounce off each-other and a dice table to come to rest with a particular result facing upwards ... in fact I don't even have a pair of dice because they are imaginary! All I can do therefore is use the above probability distribution and recognise that there is some uncertainty to its shape.
UKCP09 probabilistic data
I can confidentially describe every single possible outcome of rolling two dice. Things get more difficult if I want to describe the exact probability distribution if those dice are not perfect rollers. Climate change modellers have a massively greater challenge in trying to describe how weather patterns will change over the next hundred years. The range of possible outcomes and the probability distribution is practically impossible to grasp.
The UK Climate Projections 2009 (UKCP09) have tried to come up probability distributions though. In fact the projections are described as "probabilistic", as they are not the kind of probability curves that I can draw for simple, perfect dice rolling. Instead they describe the weight-of-evidence for each degree of change, based on: lots of different climate models, run thousands of times, and incorporating expert judgement to discount unreasonable results. The probability behind the results of this evidence base are estimated using Bayesian probability (see here for more information from UKCP09).
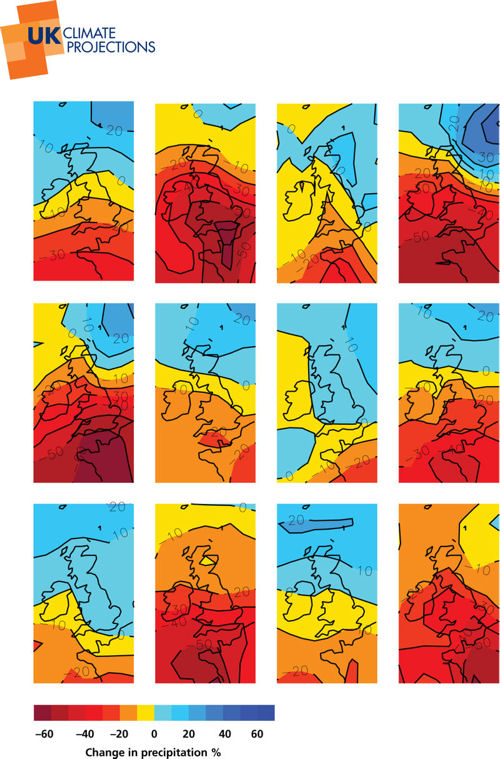
The levels of uncertainty in the climate modelling can get quite large. For example, the following figure is from Chapter 2 of the Probabilistic Projections Report, which explains how the probabilistic projections have been created in a lot of depth. Each of the maps show the results of change in summer rainfall !['precipitation' to be precise [i]](../images/_info.jpg) in the 2080s, for 12 different climate models, all using the same emission scenario. The differences are considerable for this particular weather variable and season (this is a relatively extreme example). And a lot of what we are seeing here is from different climate modellers using differing ways of trying to best model the climate system. Notice that none of them can be proven to be more real than any other model's result, and hence they all need to be taken seriously.
in the 2080s, for 12 different climate models, all using the same emission scenario. The differences are considerable for this particular weather variable and season (this is a relatively extreme example). And a lot of what we are seeing here is from different climate modellers using differing ways of trying to best model the climate system. Notice that none of them can be proven to be more real than any other model's result, and hence they all need to be taken seriously.
Choosing a range of probabilities from UKCP09
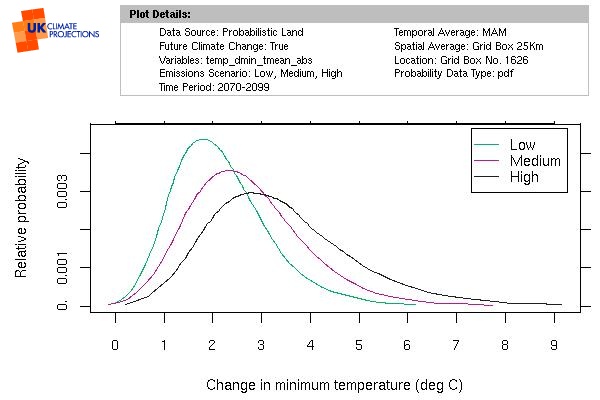
The following graph shows probability curves of low, medium and high emission scenarios, from the UK Climate Projections. ![This particular dataset shows projections of average Spring night minimum temperatures in the 2080s. [i]](../images/_info.jpg) Any of those results is possible: for example, for the low emission scenario, temperatures could be anywhere between about 0ºC and about 6ºC ... in a similar way that rolling two dice would give you a result of between 2 and 12.
Any of those results is possible: for example, for the low emission scenario, temperatures could be anywhere between about 0ºC and about 6ºC ... in a similar way that rolling two dice would give you a result of between 2 and 12.
- It is understood that there is less confidence in the range and probability of the tail ends of each curves. In fact the UKCP09 report urges the reader to use very low (e.g. less than 5%) or very high (e.g. greater than 95%) probabilities with caution.
- It is not good to just use the central estimate (i.e. the median = 50% probability) result either, as it is no more likely than any other result; and it gives no indication that there is a range of uncertainty and how wide that range is.
- What I will do therefore is pick the same band that I highlighted in the dice rolling example above: the 67% band around the central estimate. In the following graph, for the low emission scenario, this is the band of temperatures between about 1ºC and about 3.5ºC.
- We must remember that there is uncertainty in these figures as, like the imperfect dice, there is uncertainty in the exact shape of the probabilistic distribution curve.

Return to Temperatures in Reading page

![link to W3C validation website, which will show that the stylesheets are Valid CSS [css]](http://jigsaw.w3.org/css-validator/images/vcss-blue)
![link to information about this website [info]](../images/btn_info.jpg)
![jump up to the top of this page [top]](../images/btn_top.jpg)